[Algorithm] 멀쩡한사각형

멀쩡한 사각형 (Summer/Winter Coding(2019))

---

문제설명

 가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다.
 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

---

제한사항

W, H : 1억 이하의 자연수

입출력 예

W	H	result
8	12	80

---

입출력 예 설명

입출력 예 #1
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

---

문제풀이

처음에 문제를 봤을 때 바로 떠오른 생각이 최대공약수 개념이었다.
위에 있는 그림은 스크롤을 내리지 못해 미처 발견하지 못했고 혼자서 생각해보았다.

5분 정도 혼자 고민을 한 끝에 최대공약수로는 판단할 수 없다고 생각을 했다.

따라서, 구글링을 통해 [대각선이 지나는 점의 개수]를 찾는 방법을 찾았다.
[대각선이 지나는 점의 개수] : https://m.blog.naver.com/orbis1020/220664563768

초등학교 5학년의 수학문제라는 점에서 자괴감이 들었다. 나는. 4학년이니까 괜찮다! (..대학교)

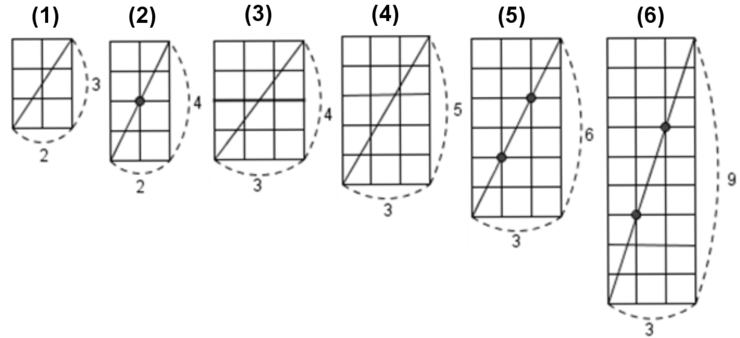
본론으로 다시 넘어와서 점의 개수는 위의 그림처럼 격자점의 유무에 따라 달라진다.

(1) 격자점이 존재할 경우 : 가로와 세로의 최대공약수가 2일 때
(2) 격자점이 존재하지 않을 경우 : 두 수의 최대공약수가 1일 때

(1)의 경우에는 '(가로)+(세로)-1'
(2)의 경우에는 '(가로)+(세로)-(가로와 세로의 최대공약수)

하지만 둘 다 코드에선 같은 최대공약수를 빼므로 결론적으론 (가로) + (세로) - (최대공약수)임을 알 수 있다.

최대 공약수를 구하는 방법은 다양한 방법이 있겠지만 Level1에서 배웠던 유클리드호제법을 사용하여 구했다. (Level1_C++_gcdlcm)

Code

#include <iostream>

using namespace std;

long long gcd(long long a, long long b)
{
    long c;

    while (b != 0)
    {
        c = a % b;
        a = b;
        b = c;
    }
    return a;
}
long long solution(int w, int h) {
    long long W = w;
    long long H = h;

    return (W * H) - ((W + H) - gcd(W, H));
}